
主要参考博文 :
引子
如果现在我们预测一个国家,比如说中国,2018 年全年的旅游收入 (美元)。因变量是中国 2018 年度的旅游收入 Y,自变量 X 我们假设存在下面两组:
- X1 = 2018 年来中国的总游客人数
- X2 = 2018 年中国政府对旅游作出的市场宣传财政支出
- X3 = a * X1 + b * X2 + c,a、b、c 是三个常数
另一组:
- X1 = 2018 年来中国的总游客人数
- X2 = 2018 年中国政府对旅游作出的市场宣传财政支出
- 2018 年人民币兑换美元平均汇率
上面两个情况,那种情况下预测得到 Y 会更准确呢?相信大家都会选第二组 X,因为从直觉来看第二组 X 有 3 个不同的变量,而每一个变量对可以为我们预测 Y 提供一些不一样的信息。而且,这 3 个变量都不是直接从其他变量转换来的。或者说,没有哪个变量能与其他变量构成一个线性组合。
反之,在第一组 X 里,只有两个变量提供了有用的信息,而第 3 个变量只是前两个变量的线性组合。不考虑这个变量直接构建模型的话,其实最终的模型中也包含了这个组合。
在第一组出现的这种情况就是两个变量的共线性(multicollinearity)。在这组变量里,有的变量与其他变量之间强相关(不一定要求所有变量之间都相关,但至少是两个)。此时第一组变量得到的模型将不如第二组变量得到的模型准确,因为第二组变量提供的信息比第一组要多。因此,在做回归分析的时候,研究如何鉴定和处理共线性很有必要。
概念和基础
维基百科的 Multicollinearity 词条 写道:
In statistics, multicollinearity (also collinearity) is a phenomenon in which one predictor variable in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy. In this situation the coefficient estimates of the multiple regression may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least within the sample data set; it only affects calculations regarding individual predictors. That is, a multivariate regression model with collinear predictors can indicate how well the entire bundle of predictors predicts the outcome variable, but it may not give valid results about any individual predictor, or about which predictors are redundant with respect to others.
多重回归时,一个自变量能被其他自变量在一定程度上线性预测时就是共线性。此时,模型或者数据中的微小的变化就可能会引起回归系数异常的变化。共线性不会降低模型整体的预测效力和可信度(在相同样本数据前提下),但它将影响对个体的预测。即,在存在共线性情况下,模型仍能反映所有自变量对因变量的预测能力,但对于单个自变量所给出的预测,或者关于自变量是否冗余的结论则都不可信。
共线性的出现可以有很多原因。比如哑变量的引入或者不正确的使用可能会导致共线性。使用通过其他变量转换生成的变量也会导致共线性,上面的例子就是这样的。另外,如果引入的变量之间本身就是相关的,或者提供的信息相似也有可能造成共线性(下面会出现例子)。共线性在总体上不会导致什么问题,但是却对单个变量及其预测效能影响巨大。它可能使得我们根本没办法鉴定哪些变量是显著性的。有时候你会发现一组变量的预测结果非常相似,或者一些变量相对其他一些变量完全就是冗余的。总结起来,共线性可能导致这些后果:
- 无法鉴定哪些变量是具有显著意义的。因为共线性会使得模型相对于所选取的样本数据十分敏感,不同的样本数据会得到不同的显著变量结果
- 因为共线性的存在使得标准差倾向于异常的大,因此也无法准确估计回归系数。选取不同的样本数据的时候,回归系数的值甚至是符号都会发生变化。
- 模型对于加入或剔除独立的变量异常敏感。添加一个与当前存在的变量正交的变量时,模型也可能会得出完全不同的结果;从模型中剔除一个变量也可能会对模型造成很大的影响。
- 可信区间变得很宽,因此可能无法拒绝备择假设。备择假设认为在总体人群中回归系数为 0 (即模型是随机事件观察到的结果)。
好的,现在我们知道共线性不是个好事。那要怎么识别共线性呢?方法有很多:
- 第一个也是最简单的就是看变量之间两两相关性。在很多情况下,变量之间多多少少都存在一些相关性。但是变量之间的高度相关性就很容易导致共线性问题了。
- 加入或者剔除变量,或者样本数据变化时回归系数变化异常的大也提示共线性的存在。使用不同的样本数据建模得到不同的显著变量也提示共线性存在。
- 另一个方法是使用方差扩大因子(或方差膨胀因子,variance inflation factor,VIF)。VIF > 10 时提示变量之间存在共线性。一般地,我们认为 VIF < 4 时模型稳定。
- 模型总体 R 方很高,但是多数变量的回归系数都不显著。这也提示模型中存在变量间共线性。
- Farrar-Glauber 检验是用于检测共线性的一种统计方法。它又包含了 3 个进一步的检验:首先是卡方检验确定系统中是否有共线性的存在;然后是方差检验(或叫 F 检验)用于发现哪些变量间存在共线性关系;最后是 t 检验确定共线性的模式和类别。
例子
下面来通过一个列子看看怎么鉴别数据中的共线性以及简单的处理。
我们用到的数据叫做 CPS_85_Wages data,来源与介绍:
These data consist of a random sample of 534 persons from the CPS, with information on wages and other characteristics of the workers, including sex, number of years of education, years of work experience, occupational status, region of residence and union membership. Source: Berndt, ER. The Practice of Econometrics. 1991. NY: Addison-Wesley. (Therese.A.Stukel_AT_Dartmouth.EDU) (MS Word format) 21/Jul/98
这里可以下载到:https://www.economicswebinstitute.org/data/wagesmicrodata.xls 。
我也上传到了 GitHub repo:wagesmicrodata.xls 。
R 的 mosaic 包也附带了这个数据,library(mosaic) 然后 data("CPS85") 就可以加载这个数据了,但是这个数据和我们直接下载的稍微形式变了一点,我嫌麻烦就直接用了 xls 文件了。但是其实 ?CPS85 查看帮助看看关于数据的细节也不错的。
简单来说,这个数据是来自 534 人的样本的薪水和其他一些信息,比如年龄、性别、人种、受教育年限、工作年限、工作状态、居住地、工会状态、婚姻状态等等。而我们现在就是想通过这一系列变量来预测薪水。
先来看看数据长什么样子:
1
2
3
4
|
# 原始数据里数据在 Sheet2,名叫 Data, 第一行第一列没用,我都直接自己删掉了
CPS85 <- readxl::read_xlsx('CPS85', sheet = 1)
str(CPS85)
|
数据这样子:
1
2
3
4
5
6
7
8
9
10
11
12
|
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 534 obs. of 11 variables:
$ WAGE : num 5.1 4.95 6.67 4 7.5 ...
$ OCCUPATION: num 6 6 6 6 6 6 6 6 6 6 ...
$ SECTOR : num 1 1 1 0 0 0 0 0 1 0 ...
$ UNION : num 0 0 0 0 0 1 0 0 0 0 ...
$ EDUCATION : num 8 9 12 12 12 13 10 12 16 12 ...
$ EXPERIENCE: num 21 42 1 4 17 9 27 9 11 9 ...
$ AGE : num 35 57 19 22 35 28 43 27 33 27 ...
$ SEX : num 1 1 0 0 0 0 0 0 0 0 ...
$ MARR : num 1 1 0 0 1 0 0 0 1 0 ...
$ RACE : num 2 3 3 3 3 3 3 3 3 3 ...
$ SOUTH : num 0 0 0 0 0 0 1 0 0 0 ...
|
更直观一点:
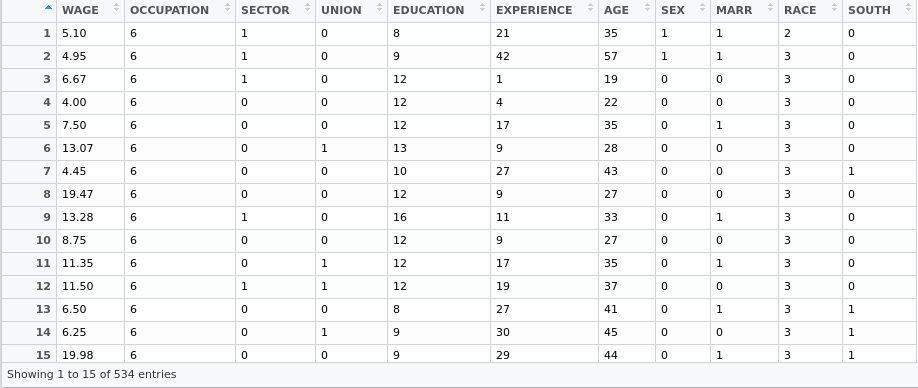
首先我们先用所有变量建立线性模型。这里,由于薪水之间差别很大导致方差也会很大,我们把它 Log 一下。
1
|
fit1 = lm(log(CPS85$WAGE) ~., data = CPS85)
|
看看效果如何 summary(fit1):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
Call:
lm(formula = log(CPS85$WAGE) ~ ., data = CPS85)
Residuals:
Min 1Q Median 3Q Max
-2.1625 -0.2916 -0.0047 0.2998 1.9825
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.07860 0.68751 1.57 0.11729
OCCUPATION -0.00742 0.01311 -0.57 0.57176
SECTOR 0.09146 0.03874 2.36 0.01859 *
UNION 0.20048 0.05247 3.82 0.00015 ***
EDUCATION 0.17937 0.11076 1.62 0.10595
EXPERIENCE 0.09582 0.11080 0.86 0.38753
AGE -0.08544 0.11073 -0.77 0.44067
SEX -0.22200 0.03991 -5.56 4.2e-08 ***
MARR 0.07661 0.04193 1.83 0.06826 .
RACE 0.05041 0.02853 1.77 0.07787 .
SOUTH -0.10236 0.04282 -2.39 0.01719 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.44 on 523 degrees of freedom
Multiple R-squared: 0.318, Adjusted R-squared: 0.305
F-statistic: 24.4 on 10 and 523 DF, p-value: <2e-16
|
R 方 0.318,对于一个 只有 534 个样本的数据来说还行。F 统计量高度显著,提示模型中多个变量对因变量的解释具有统计学意义。但仔细看的话会发现 4 个变量 (occupation, education, experience, age) 没有统计学意义,有 2 个变量 (marital status 及 south) 在 0.1 的统计学水平上有显著性。
下面我们来画图看看模型诊断信息所反映的误差正态性、方差齐性等等:
1
2
|
par(mfrow=c(2,2))
plot(fit1)
|
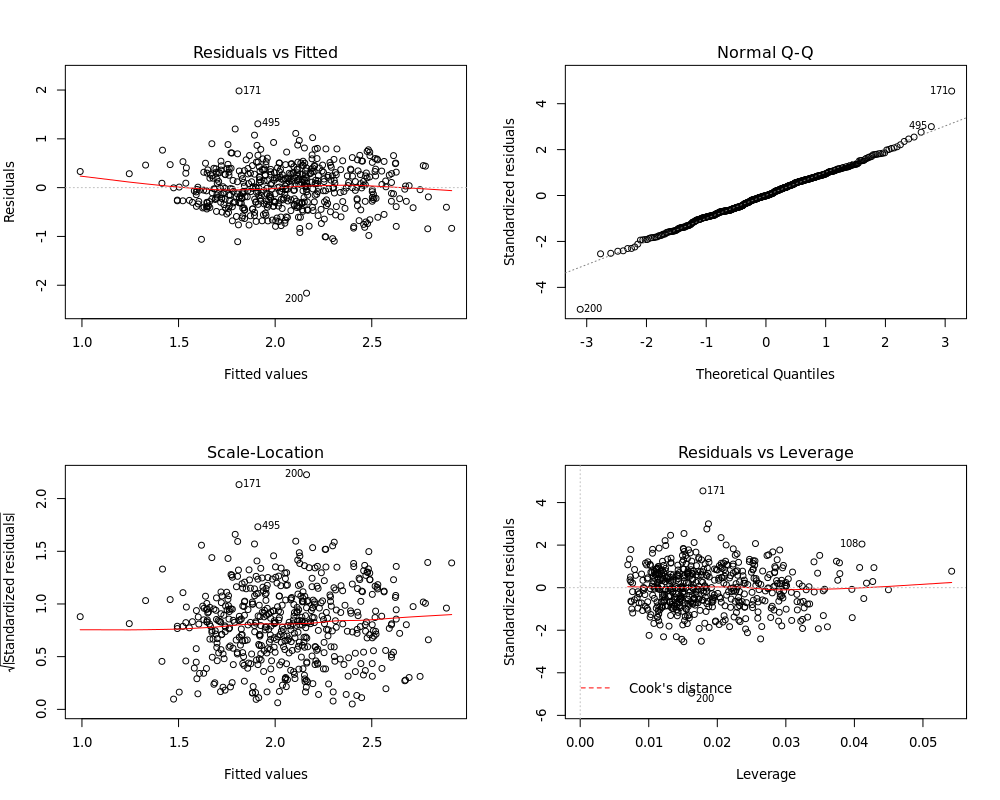
图看着也还行。所以问题可能在于得到的显著变量为什么这么少。
进一步,我们看看变量间的关系:
1
2
|
library(GGally)
ggpairs(X)
|
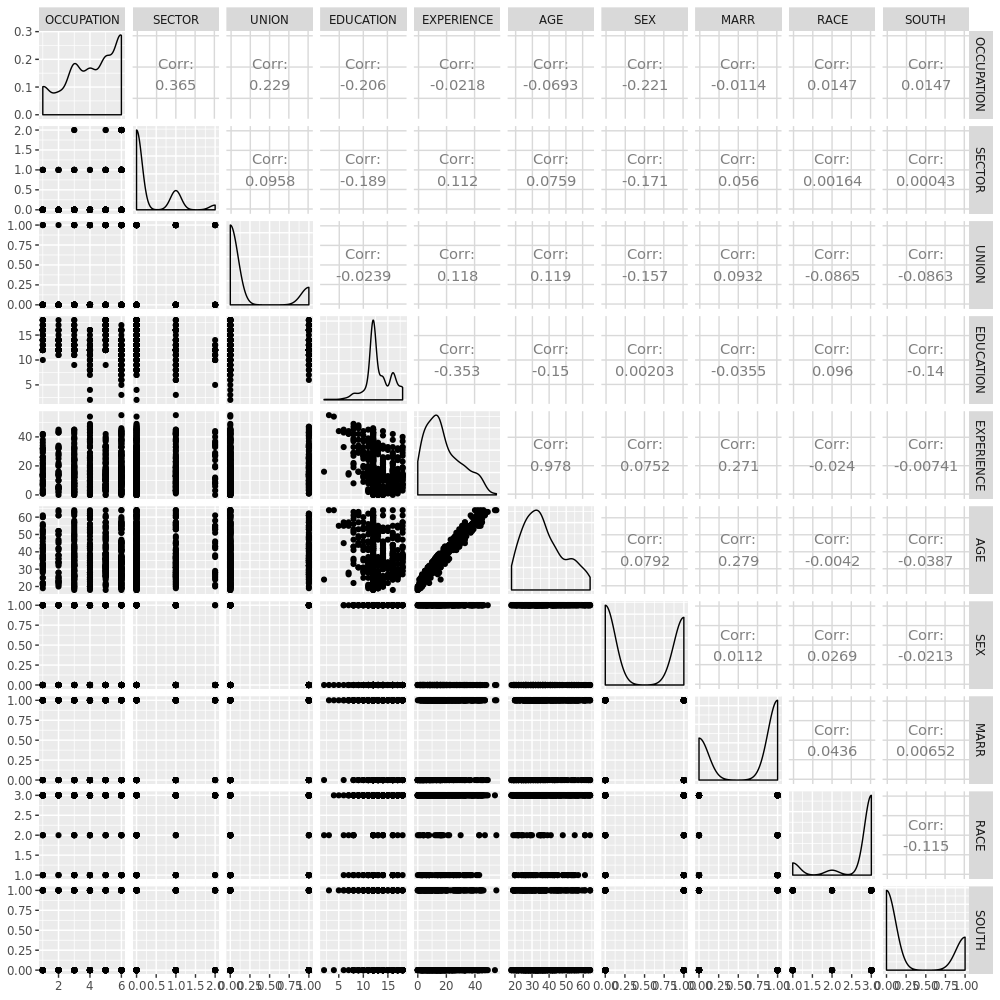
或者
1
2
3
4
|
library(corrplot)
cor1 <- cor(CPS85)
corrplot.mixed(cor1, lower.col = 'black', cl.cex = 0.8, tl.cex = 0.8)
|
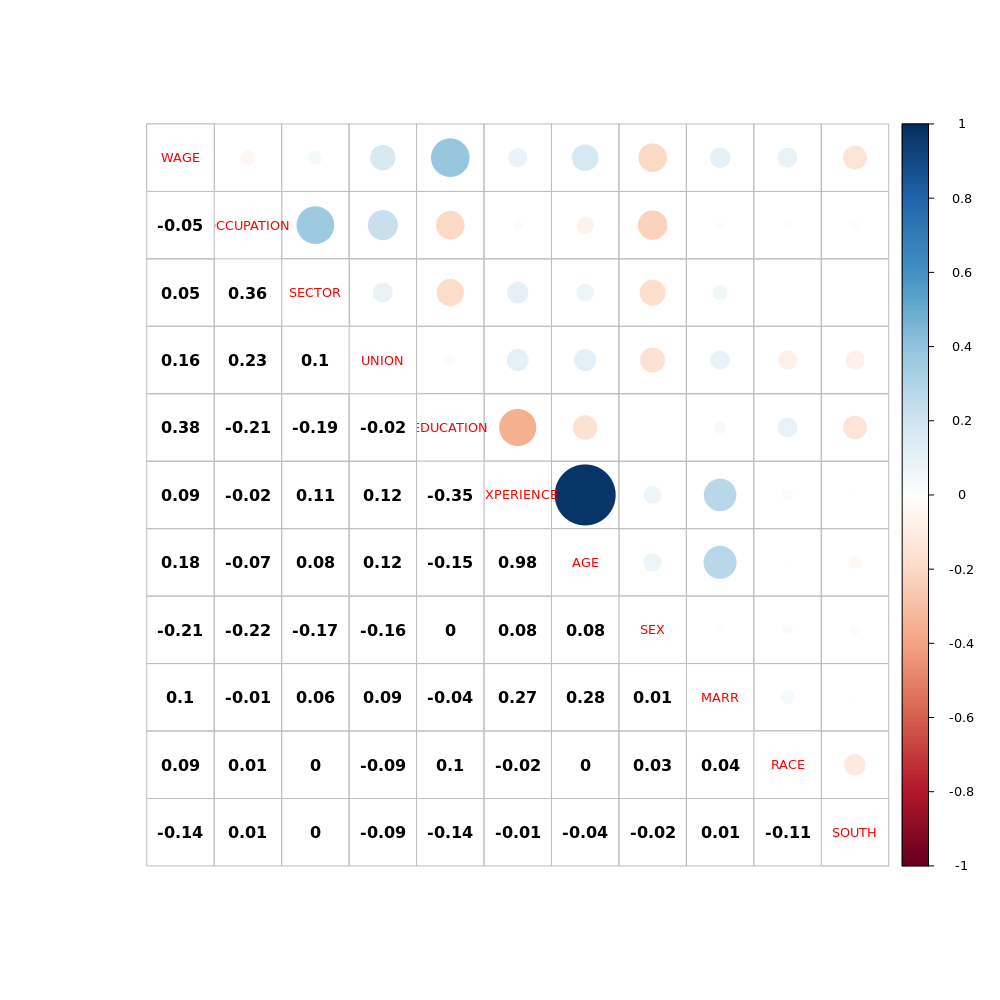
从两张图都可以发现,AGE 和 EXPERIENCE 以及 EDUCATION 之间关联性很高。来看看偏相关系数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
library(corpcor)
corpcor::cor2pcor(cov(CPS85[,-1]))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1.000000 0.314747 0.212996 0.029437 0.04206 -0.04414 -0.142751 -0.018581 0.057539 0.008431
[2,] 0.314747 1.000000 -0.013531 -0.021253 -0.01326 0.01457 -0.112147 0.036495 0.006412 -0.021519
[3,] 0.212996 -0.013531 1.000000 -0.007479 -0.01024 0.01224 -0.120088 0.068918 -0.107706 -0.097549
[4,] 0.029437 -0.021253 -0.007479 1.000000 -0.99756 0.99726 0.051510 -0.040303 0.017231 -0.031750
[5,] 0.042059 -0.013262 -0.010244 -0.997562 1.00000 0.99988 0.054977 -0.040977 0.010888 -0.022314
[6,] -0.044140 0.014566 0.012239 0.997262 0.99988 1.00000 -0.053698 0.045090 -0.010803 0.021525
[7,] -0.142751 -0.112147 -0.120088 0.051510 0.05498 -0.05370 1.000000 0.004163 0.020017 -0.030152
[8,] -0.018581 0.036495 0.068918 -0.040303 -0.04098 0.04509 0.004163 1.000000 0.055646 0.030418
[9,] 0.057539 0.006412 -0.107706 0.017231 0.01089 -0.01080 0.020017 0.055646 1.000000 -0.111198
[10,] 0.008431 -0.021519 -0.097549 -0.031750 -0.02231 0.02153 -0.030152 0.030418 -0.111198 1.000000
colnames(CPS85[,-1])
[1] "OCCUPATION" "SECTOR" "UNION" "EDUCATION" "EXPERIENCE" "AGE" "SEX" "MARR"
[9] "RACE" "SOUTH
|
一样的,我们发现 AGE 和 EXPERIENCE 以及 EDUCATION 之间关联性很高。
接下来,我们来做 Farrar-Glauber 检验看看。mctest 包的 omcdiag (Overall Multicollinearity Diagnostics Measures) 函数计算不同的检测总体共线性的指标:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
library(mctest)
omcdiag(CPS85[, -1], CPS85$WAGE)
Call:
omcdiag(x = CPS85[, -1], y = CPS85$WAGE)
Overall Multicollinearity Diagnostics
MC Results detection
Determinant |X'X|: 0.000 1
Farrar Chi-Square: 4833.575 1
Red Indicator: 0.198 0
Sum of Lambda Inverse: 10068.844 1
Theil's Method: 1.226 1
Condition Number: 739.734 1
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the test |
结果表明模型中存在共线性的现象。然后是 F 检验看看具体哪些变量的问题:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
imcdiag(CPS85[, -1], CPS85$WAGE)
Call:
imcdiag(x = CPS85[, -1], y = CPS85$WAGE)
All Individual Multicollinearity Diagnostics Result
VIF TOL Wi Fi Leamer CVIF Klein
OCCUPATION 1.298 0.770 1.736e+01 1.957e+01 0.878 1.328 0
SECTOR 1.199 0.834 1.157e+01 1.304e+01 0.913 1.226 0
UNION 1.121 0.892 7.037e+00 7.931e+00 0.945 1.146 0
EDUCATION 231.196 0.004 1.340e+04 1.511e+04 0.066 236.473 1
EXPERIENCE 5184.094 0.000 3.018e+05 3.401e+05 0.014 5302.419 1
AGE 4645.665 0.000 2.704e+05 3.048e+05 0.015 4751.700 1
SEX 1.092 0.916 5.335e+00 6.013e+00 0.957 1.117 0
MARR 1.096 0.912 5.597e+00 6.309e+00 0.955 1.121 0
RACE 1.037 0.964 2.162e+00 2.437e+00 0.982 1.061 0
SOUTH 1.047 0.955 2.726e+00 3.073e+00 0.977 1.071 0
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the test
OCCUPATION , SECTOR , EDUCATION , EXPERIENCE , AGE , MARR , RACE , SOUTH , coefficient(s) are non-significant may be due to multicollinearity
R-square of y on all x: 0.28
* use method argument to check which regressors may be the reason of collinearity
===================================
|
VIF、TOL 和 Wi 列分别为 variance inflation factor, tolerance 和 Farrar-Glauber F 检验结果。
检验结果显示 EDUCATION,EXPERIENCE 和 AGE 确实存在共线性,而且 VIF 也确实很大。
最后 t 检验看看是什么样的关系:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
library(ppcor)
pcor(CPS85[,-1], method = "pearson")
$estimate
OCCUPATION SECTOR UNION EDUCATION EXPERIENCE AGE SEX MARR RACE SOUTH
OCCUPATION 1.000000 0.314747 0.212996 0.029437 0.04206 -0.04414 -0.142751 -0.018581 0.057539 0.008431
SECTOR 0.314747 1.000000 -0.013531 -0.021253 -0.01326 0.01457 -0.112147 0.036495 0.006412 -0.021519
UNION 0.212996 -0.013531 1.000000 -0.007479 -0.01024 0.01224 -0.120088 0.068918 -0.107706 -0.097549
EDUCATION 0.029437 -0.021253 -0.007479 1.000000 -0.99756 0.99726 0.051510 -0.040303 0.017231 -0.031750
EXPERIENCE 0.042059 -0.013262 -0.010244 -0.997562 1.00000 0.99988 0.054977 -0.040977 0.010888 -0.022314
AGE -0.044140 0.014566 0.012239 0.997262 0.99988 1.00000 -0.053698 0.045090 -0.010803 0.021525
SEX -0.142751 -0.112147 -0.120088 0.051510 0.05498 -0.05370 1.000000 0.004163 0.020017 -0.030152
MARR -0.018581 0.036495 0.068918 -0.040303 -0.04098 0.04509 0.004163 1.000000 0.055646 0.030418
RACE 0.057539 0.006412 -0.107706 0.017231 0.01089 -0.01080 0.020017 0.055646 1.000000 -0.111198
SOUTH 0.008431 -0.021519 -0.097549 -0.031750 -0.02231 0.02153 -0.030152 0.030418 -0.111198 1.000000
$p.value
OCCUPATION SECTOR UNION EDUCATION EXPERIENCE AGE SEX MARR RACE SOUTH
OCCUPATION 0.000e+00 1.467e-13 8.220e-07 0.5005 0.3357 0.3123 0.001027 0.6707 0.18764 0.84704
SECTOR 1.467e-13 0.000e+00 7.569e-01 0.6267 0.7616 0.7389 0.010051 0.4035 0.88336 0.62243
UNION 8.220e-07 7.569e-01 0.000e+00 0.8641 0.8147 0.7794 0.005823 0.1144 0.01345 0.02527
EDUCATION 5.005e-01 6.267e-01 8.641e-01 0.0000 0.0000 0.0000 0.238259 0.3563 0.69338 0.46745
EXPERIENCE 3.357e-01 7.616e-01 8.147e-01 0.0000 0.0000 0.0000 0.208090 0.3483 0.80325 0.60963
AGE 3.123e-01 7.389e-01 7.794e-01 0.0000 0.0000 0.0000 0.218884 0.3020 0.80476 0.62233
SEX 1.027e-03 1.005e-02 5.823e-03 0.2383 0.2081 0.2189 0.000000 0.9241 0.64692 0.49016
MARR 6.707e-01 4.035e-01 1.144e-01 0.3563 0.3483 0.3020 0.924111 0.0000 0.20260 0.48635
RACE 1.876e-01 8.834e-01 1.345e-02 0.6934 0.8033 0.8048 0.646920 0.2026 0.00000 0.01071
SOUTH 8.470e-01 6.224e-01 2.527e-02 0.4675 0.6096 0.6223 0.490163 0.4863 0.01071 0.00000
$statistic
OCCUPATION SECTOR UNION EDUCATION EXPERIENCE AGE SEX MARR RACE SOUTH
OCCUPATION 0.0000 7.5907 4.9902 0.6741 0.9636 -1.0114 -3.3015 -0.4254 1.3193 0.1930
SECTOR 7.5907 0.0000 -0.3098 -0.4866 -0.3036 0.3335 -2.5835 0.8360 0.1468 -0.4927
UNION 4.9902 -0.3098 0.0000 -0.1712 -0.2345 0.2802 -2.7690 1.5814 -2.4799 -2.2437
EDUCATION 0.6741 -0.4866 -0.1712 0.0000 -327.2105 308.6803 1.1807 -0.9233 0.3945 -0.7272
EXPERIENCE 0.9636 -0.3036 -0.2345 -327.2105 0.0000 1451.9092 1.2604 -0.9388 0.2493 -0.5109
AGE -1.0114 0.3335 0.2802 308.6803 1451.9092 0.0000 -1.2310 1.0332 -0.2473 0.4928
SEX -3.3015 -2.5835 -2.7690 1.1807 1.2604 -1.2310 0.0000 0.0953 0.4583 -0.6905
MARR -0.4254 0.8360 1.5814 -0.9233 -0.9388 1.0332 0.0953 0.0000 1.2758 0.6966
RACE 1.3193 0.1468 -2.4799 0.3945 0.2493 -0.2473 0.4583 1.2758 0.0000 -2.5613
SOUTH 0.1930 -0.4927 -2.2437 -0.7272 -0.5109 0.4928 -0.6905 0.6966 -2.5613 0.0000
$n
[1] 534
$gp
[1] 8
$method
[1] "pearson"
|
和前面结果一致,EDUCATION,EXPERIENCE 和 AGE 三个变量 p 值显著,三者之间偏相关系数接近 1 。
同时发现其实有的相关性很低的变量之间相关性也是显著的。
现在我们明白状况了,那接下来要怎么办呢?解决的办法很多,比如主成分回归,岭回归和逐步回归等等。
这里呢,我们简单点,直接选一个 VIF > 10 的变量剔除出去看看。显然,年龄和工作经验这个肯定是高度相关的,没必要两个都纳入模型。年龄本身就可以反映工作经验。我们直接把 EXPERIENCE 剔除掉然后看看模型怎么样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
fit2<- lm(log(WAGE) ~ OCCUPATION + SECTOR + UNION + EDUCATION + AGE + SEX + MARR + RACE+SOUTH, data = CPS85)
summary(fit2)
Call:
lm(formula = log(WAGE) ~ OCCUPATION + SECTOR + UNION + EDUCATION +
AGE + SEX + MARR + RACE + SOUTH, data = CPS85)
Residuals:
Min 1Q Median 3Q Max
-2.1602 -0.2908 -0.0051 0.2999 1.9793
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.50136 0.16479 3.04 0.00247 **
OCCUPATION -0.00694 0.01309 -0.53 0.59631
SECTOR 0.09101 0.03872 2.35 0.01912 *
UNION 0.20002 0.05246 3.81 0.00015 ***
EDUCATION 0.08381 0.00773 10.85 < 2e-16 ***
AGE 0.01031 0.00175 5.91 6.3e-09 ***
SEX -0.22010 0.03984 -5.52 5.2e-08 ***
MARR 0.07512 0.04189 1.79 0.07346 .
RACE 0.05067 0.02852 1.78 0.07621 .
SOUTH -0.10319 0.04280 -2.41 0.01626 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.44 on 524 degrees of freedom
Multiple R-squared: 0.318, Adjusted R-squared: 0.306
F-statistic: 27.1 on 9 and 524 DF, p-value: <2e-16
|
现在 9 个变量里大部分都是显著的,而且 F 检验也显示没什么问题。我们再检查下 VIF:
1
2
3
|
car::vif(fit2)
OCCUPATION SECTOR UNION EDUCATION AGE SEX MARR RACE SOUTH
1.296 1.198 1.121 1.126 1.154 1.088 1.094 1.037 1.046
|
嗯,现在所有变量 VIF < 4,共线性问题没了。
虽然博客看懂了,代码也都照做并且确实解决了共线性问题,但其实这里面涉及到的统计方法我都不是很熟悉,只能算是一知半解吧。有空还是要好好看看这部分的统计基础,以及 mctest 的 Manual 要看看。另外这里只涉及到了连续变量的共线性,实际中肯定要碰到分类变量以及等级变量的,这个还要学习。




